


Next: Structural Alignment algorithm based
Up: Efficient algorithms for Local
Previous: Introduction
Problem Definition of Local structural alignment
INPUT: Given two protein structures
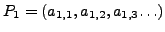 and
and
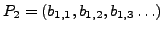 where
where 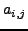 represents
represents
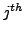 atom of
atom of 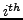 residue
residue 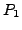 and
and 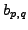 is
is 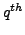 atom
in
atom
in 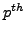 residue of
residue of 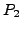 . The value in
. The value in 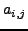 and
and 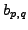 corresponds to 3D-coordinate of that atom,
corresponds to 3D-coordinate of that atom,
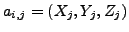 and
and
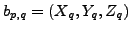 .
.
OUTPUT: Define correspondence between 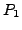 and
and 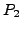 as
as
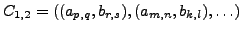 , the Local
structural alignment problem asks to find a correspondence
(
, the Local
structural alignment problem asks to find a correspondence
(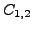 ) between
) between 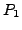 ,
,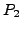 along with a rotational matrix
along with a rotational matrix 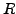 and
translation matrix
and
translation matrix 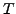 such that when you apply
such that when you apply 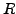 and
and 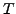 to one set
of coordinates (
to one set
of coordinates (
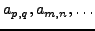 ) we would be able to produce
the other set in the correspondence (
) we would be able to produce
the other set in the correspondence (
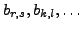 ), the
optimization version asks for
), the
optimization version asks for 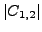 to be maximal.
to be maximal.
Vamsi Kundeti
2007-10-10