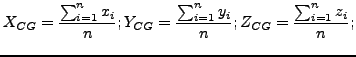Center of Gravity based algorithm

The key idea behind our structural alignment algorithm is based on the following theorem.

Theorem 1   Given two 3-D pointsets $S_1$ ,$S_2$ each of size $n$ , $S_1=\{({x^1}_1,{y^1}_1,{z^1}_1),({x^1}_2,{y^1}_2,{z^1}_2),{\ldots}\}$ and $S_2=\{({x^2}_1,{y^2}_1,{z^2}_1)({x^2}_2,{y^2}_2,{z^2}_2),\ldots\}$ . We can check if $S_1$ is a rigid transformation of $S_2$ in $O(nlog(n))$ time and $O(n)$ space

Proof. The proof is based on a very simple fact that relative position(from any of the points in the point set) of the Center of Gravity of a set of 3-D points remains unchanged when these 3-D points are transformed by any rigid transformation. The Center of Gravity(CG) for a 3-D point sets is defined as follows.

$$S_1=\{({x}_1,{y}_1,{z}_1),({x}_2,{y}_2,{z}_2),{\ldots}\};$$

$$X_{CG} = \frac{\sum_{i=1}^{n}x_i}{n}; \\ Y_{CG} = \frac{\sum_{i=1}^{n}y_i}{n}; \\ Z_{CG} = \frac{\sum_{i=1}^{n}z_i}{n};$$

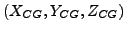
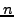
If the relative position of the CG with respect any of the points in the point set changes due to transformation then the transformation is not a rigid transformation. So we use this fact and compute the euclidean distance from $(X_{CG},Y_{CG},Z_{CG})$ to each of the $n$ points in the point set call this distance ${d_{i}}^{cg}$ .

$${d_{i}}^{cg} = \sqrt{(X_{CG}-x_i)^2+(Y_{CG}-y_i)^2+(Z_{CG}-y_i)^2}$$

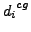
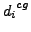
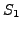
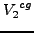
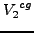
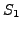
once we compute ${d_{i}}^{cg}$ we sort these distances and create a distance vector ${V_{1}}^{cg}$ for point set $S_1$ similarly we create a vector ${V_{2}}^{cg}$ for $S_2$ . 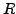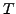And finally compare if ${V_{1}}^{cg}$ and ${V_{2}}^{cg}$ are the same if they are same its possible to find a rigid transformation from $S_1$ to $S_2$ , once we know that its possible to find a rigid transformation its trivial to find out $R$ (rotational) and $T$ (translational). $\qedsymbol$

The Algorithm1 is based on Theorem1 boxed