


Next: Center of Gravity based
Up: Structural Alignment algorithm based
Previous: Description of protein structure
From the problem definition in the section2
which asks to
find correspondence 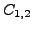 between
between 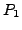 and
and 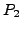 (assume each
of length of
(assume each
of length of 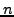 ), a naive algorithm to find a correspondence of
length of
), a naive algorithm to find a correspondence of
length of  would test each of
would test each of 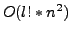 correspondences
to see if it can find a rigid transformation
correspondences
to see if it can find a rigid transformation 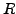 (Rotational),
(Rotational),
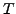 (Transformational) which can transform one set in the correspondence
to the other set, and to find the correspondence with maximum
(Transformational) which can transform one set in the correspondence
to the other set, and to find the correspondence with maximum  we to
try for all the possible
we to
try for all the possible
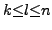 and hence the naive algorithm
needs to generate all
and hence the naive algorithm
needs to generate all
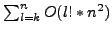 correspondences and
for each of such correspondence check if there is a rigid transformation
correspondences and
for each of such correspondence check if there is a rigid transformation
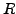 and
and 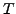 which can transform one set to the other, note the
which can transform one set to the other, note the 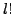 comes from ordering of the atoms in each of the residue, as we described in the section3.1 the atoms in each residue
can be ordered in any
order so we need to consider all the
comes from ordering of the atoms in each of the residue, as we described in the section3.1 the atoms in each residue
can be ordered in any
order so we need to consider all the 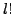 orderings. Now we have
addressed the complexity of the problem and lets see how we can solve
this in the next section.
orderings. Now we have
addressed the complexity of the problem and lets see how we can solve
this in the next section.



Next: Center of Gravity based
Up: Structural Alignment algorithm based
Previous: Description of protein structure
Vamsi Kundeti
2007-10-10